Компьютерная модель фазовращателя

Компьютерная модель фазовращателя

Для управления генерируемой частотой в компьютерной модели преобразователя необходим фазовращатель. Компьютерная модель фазовращателя в программе MatLab в среде Simulink была разработана самостоятельно.
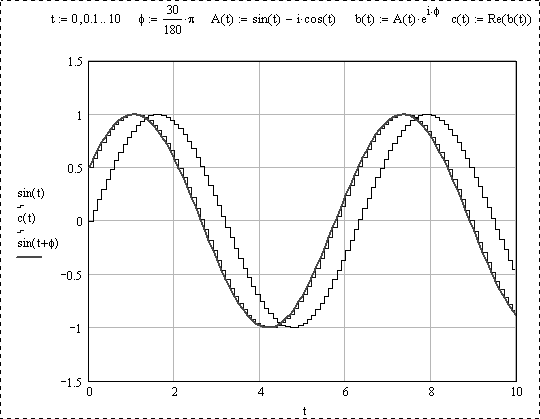
Принцип работы фазовращателя состоит в следующем. Берется гармонический синусоидальный сигнал sin(wt). Выполняется его фазовый сдвиг на девяносто градусов: sin= - cos. Далее считаем, что входной сигнал sin() – это действительная часть сигнала А(t), а -cos() – это мнимая часть сигнала А(t): А(t)= sin()-icos(). Для получения необходимого фазового сдвига полученную величину А(t) необходимо умножить на единичный вектор и из полученной величины выделить действительную часть: Re(A(t) ).
Re ((a+ib)(c + id))=Re(ac-bd +i (bc + da))= ac-bd.
Временные диаграммы фазовращателя приведены на Рис. 7.

Рис. 7.

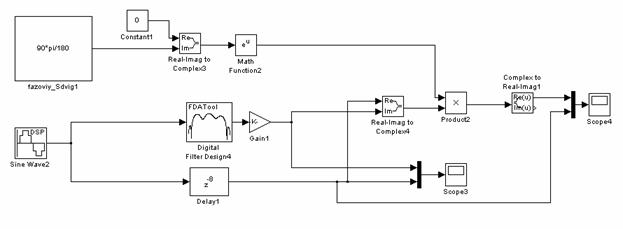
Для получения в сигнале sin(wt) фазового сдвига в 900 используется КИХ-фильтр с антисимметричной импульсной характеристикой (Рис. 8. блок Digital Filter Design). ФЧХ такого фильтра имеет наклон:
j(f)=90-kf,
где коэффициент k=,
– средняя частота КИХ-фильтра, Гц.
– частота дискретизации КИХ-фильтра, Гц.
Чтобы сигнал имел постоянный фазовый сдвиг на всех частотах sin() сигнал sin(wt) задерживается на количество отсчетов для получения эквивалентной ФЧХ (Рис. 8. блок Delay1) вида j(f)= -kf.

Рис. 8.

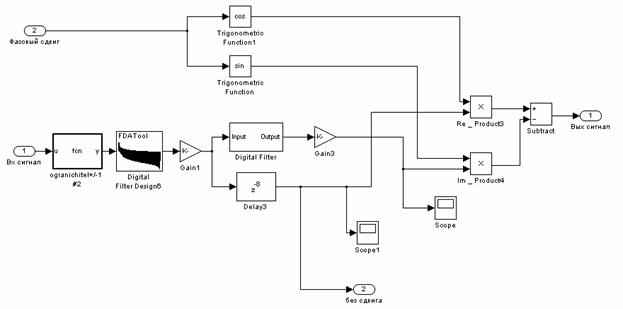
После упрощения системы (Рис. 8.) для получения быстродействия окончательная блок схема представлена на Рис. 9. Входной сигнал проходит через ограничитель (ogranichitel +/-1 #2) по амплитуде до ± 1. Далее из сигнала удаляются высокочастотные составляющие с помощью полосового цифрового КИХ - фильтра (Digital Filter Design6). Полученный сигнал нормируется до единичной амплитуды усилителем Gain1. Полученный сигнал пропускается через цифровой КИХ-фильтр (Digital Filter) с антисимметричной импульсной характеристикой и нормируется до единичной амплитуды (Gain3). На второй вход схемы подается величина фазового сдвига сигнала. От значения величины фазового сдвига рассчитывается значение sin() и cos(). Далее производится cos() с задержанным сигналом и sin() с отфильтрованным сигналом. Из первого результирующего значения производится вычитание второго результирующего значения (Substract).
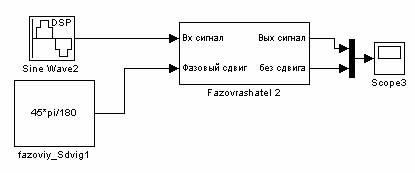
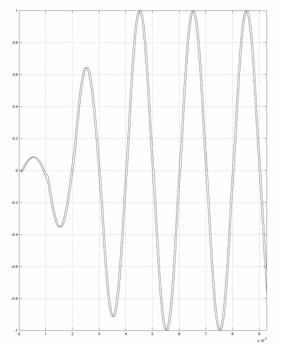
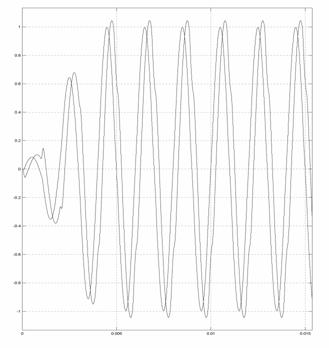
Разработанная схема (Рис. 9.) была опробована подачей гармонического сигнала любой частоты (Рис. 10.), попадающей в полосу частот полосового цифрового КИХ - фильтра (Digital Filter Design6) (Рис. 9.), и величины фазового сдвига. Результаты при величине фазового сдвига 10 градусов и 45 градусов приведены на Рис. 11.

Рис. 9.

Рис. 10.

а)

б)

Рис. 11.

TEL 8-917-828-1234